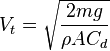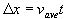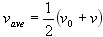Right then I have done a spreadsheet that does the calculations. It can be found here
Click Me.
The sheet uses macros so these need to be enabled. Change the items in green to calculate your shell flight. Change the items in blue if you know what the code does.
The code is rough and ready so silly values in the green boxes won't resolve and it will lock in a terminal loop. I will sort this out if I get time at some point.
I will upload an explanation of the maths over the next week or so.
A few interesting points I noticed whilst doing the program are:
1.)The smaller shells will go into the low drag coefficient range with high Reynolds numbers.
2.)The smaller shells do not approach terminal velocity before they hit the ground!
3.)The larger the shell the up and down times start to approach equal time!
Anyway the answer to the problem is just below 170m assuming that the shell weight was 150 grams.
Well have a play and look at the code to see if you can find any errors or even optimise it (plenty of scope for optimisation).
Phew that was close.