42 replies to this topic

[Crazy Cat]

Vertical Trajectory, Freefall and General Ballistic Trajectory. http://hyperphysics....hbase/traj.html

Projectile Trajectory Computer Simulation: 60mm mortar at 150 m/s (336 mph) http://www.tinafad.com/projectile/

[digger]

Vertical Trajectory, Freefall and General Ballistic Trajectory. http://hyperphysics....hbase/traj.html

Projectile Trajectory Computer Simulation: 60mm mortar at 150 m/s (336 mph) http://www.tinafad.com/projectile/

 

None of the above are valid for real world simulation as drag is not included.

[Crazy Cat]

None of the above are valid for real world simulation as drag is not included.

You have NOT bothered to interpret my post, or read through?

Simulation Limitations: Assumes zero aerodynamic drag. This makes the simulation less accurate for high launch speeds (the higher the speed, the higher the aerodynamic drag) and small projectiles (the smaller the projectile, the larger the surface area / mass volume, the larger the aerodynamic drag relative to the kinetic energy - an M16 bullet and an 88mm shell have the same muzzle velocity, but the 88mm shell has a far greater range). http://www.tinafad.com/projectile/

Determining the aerodynamic drag coefficient of a particular mortar shell based on its surface area to mass volume ratio, would have to be determined experimentally, and applied into the formula.

Effect of air Resistance. http://www.splung.co...age/projectiles

Pro Ballistic Trajectory Computer. http://ballisticapp.com/

Attached Files

•  Going Ballistic_ Bullet Trajectories.pdf   492.86KB   856 downloads

Edited by Crazy Cat, 23 October 2014 - 11:24 PM.

[digger]

You have NOT bothered to interpret my post, or read through?

Simulation Limitations: Assumes zero aerodynamic drag. This makes the simulation less accurate for high launch speeds (the higher the speed, the higher the aerodynamic drag) and small projectiles (the smaller the projectile, the larger the surface area / mass volume, the larger the aerodynamic drag relative to the kinetic energy - an M16 bullet and an 88mm shell have the same muzzle velocity, but the 88mm shell has a far greater range). http://www.tinafad.com/projectile/

Determining the aerodynamic drag coefficient of a particular mortar shell based on its surface area to mass volume ratio, would have to be determined experimentally, and applied into the formula.

Effect of air Resistance. http://www.splung.co...age/projectiles

Pro Ballistic Trajectory Computer. http://ballisticapp.com/

Yes i did read it.

 

I have not read your latest links. Drag can be accounted for easily in the case of spherical shells. It is a simple matter of understanding the relationship of Reynolds number vs velocity of the shell. In fact I wrote a simulation for this skme years ago and published it.

 

If you would like a copy I will post it here.

[digger]

Useful stuff that mr Reynolds came up with. I still use his work a lot in the day job, not wing sections though.

[Crazy Cat]

Yes i did read it.
 
I have not read your latest links. Drag can be accounted for easily in the case of spherical shells. It is a simple matter of understanding the relationship of Reynolds number vs velocity of the shell. In fact I wrote a simulation for this skme years ago and published it.

Yes, the "Reynolds Number" The boundary layer is very important in determining the drag of an object. To determine and predict these conditions, aerodynamicists rely on wind tunnel testing and very sophisticated computer analysis.

Reynolds Number - online calculators.

As an object moves through the atmosphere, the gas molecules of the atmosphere near the object are disturbed and move around the object. Aerodynamic forces are generated between the gas and the object. The magnitude of these forces depend on the shape of the object, the speed of the object, the mass of the gas going by the object and on two other important properties of the gas; the viscosity, or stickiness, of the gas and the compressibility, or springiness, of the gas. To properly model these effects, aerodynamicists use similarity parameters which are ratios of these effects to other forces present in the problem. If two experiments have the same values for the similarity parameters, then the relative importance of the forces are being correctly modeled. Representative values for the properties of air are given on another page, but the actual value of the parameter depends on the state of the gas and on the altitude.
The boundary layer is very important in determining the drag of an object. To determine and predict these conditions, aerodynamicists rely on wind tunnel testing and very sophisticated computer analysis.
http://www.grc.nasa....e/reynolds.html

http://www.engineeri...mber-d_237.html
https://www.easycalc...olds-number.php

If you would like a copy I will post it here.

Thanks, but no thanks. There's this Pro Ballistic Trajectory Computer. http://ballisticapp.com/

[digger]

You certainly are good at searching the web (after the fact).

 

Here is one for you, by the way this one is actually useful for pyrotechnics for testing lift powders and tuning shell heights.

 

Given Shell diameter, mass, time of flight from mortar and back to ground (assume it is a dummy). Develop a series of equations to determine apogee, time to apogee, muzzle velocity and impact velocity. Also propose a way of solving the system.

 

It would be interesting if it not just a series of links, but a derivation.

 

As a useful hint, for a spherical object Reynolds number is well defined empirically this makes computer analysis relatively simple as there is lots of published data for this. Maybe you should search for information on aerodynamics of spheres!

[Crazy Cat]

You certainly are good at searching the web (after the fact).

Well, your posts so-far have been simple, with little applied information. If you have the relevant information, then post, it will save me having to search?

 
Here is one for you, by the way this one is actually useful for pyrotechnics for testing lift powders and tuning shell heights.
 
Given Shell diameter, mass, time of flight from mortar and back to ground (assume it is a dummy). Develop a series of equations to determine apogee, time to apogee, muzzle velocity and impact velocity. Also propose a way of solving the system.
 
It would be interesting if it not just a series of links, but a derivation.

In the scientific community, that's called coat-tailing.
Maybe later on? I'm surprised, that a repository of data, links, spreadsheet calculators, ISN'T available to member here already?

As a useful hint, for a spherical object Reynolds number is well defined empirically this makes computer analysis relatively simple as there is lots of published data for this. Maybe you should search for information on aerodynamics of spheres!

Drag of a Sphere. http://www.grc.nasa....dragsphere.html
The drag coefficient is a dimensionless number that characterizes all of the complex factors that affect drag. The drag coefficient is usually determined experimentally using a model in a wind tunnel. In the tunnel, the velocity, density, and size of the model are known. Measuring the drag then determines the value of the drag coefficient as given by the above equation.
But for a simple sphere, the value of the drag coefficient varies widely with Reynolds number as shown on the figure at the top of this page.

 
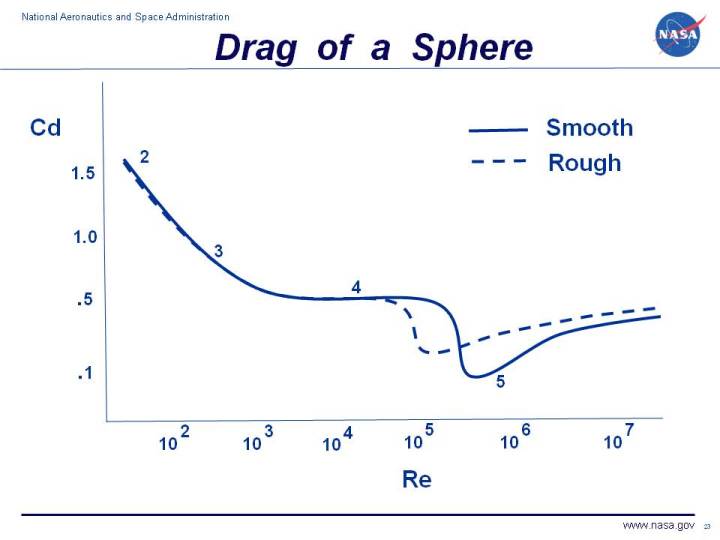
Aerodynamics of Spheres. http://www.narcap.or..._2.1_aerody.pdf

[digger]

Can't do it then?

 

By the way I did say it was published and I did ask if you would like me to post it, but you decided it was not necessary.

 

The equations are simple, it just takes a bit of thought about the solution method.

 

Anyway for those who actually might be interested, see the attached shell height calculator. There are some variables that can be played with, for instance the drag table can be extended to improve number of data points.

 

 

Attached Files

•  shell height.xls   39.5KB   375 downloads

[dave]

changing the velocity and shell diameter and pressing calculate does not seem to do anything

 

??

[digger]

Ok, the velocity is just an initial estimate, if you will a starting point for the iterations to start, so this has no effect on the final result other than to change the time to convergence for the maths (better guess = faster). I could have used a logarithmic iteration, but it is not really required as the worst that could happen is a delay of a minute or so.

 

Items in green determine the result, items in blue change accuracy and convergence rate and items in orange should only be changed for unusual firing locations.

 

Changing the shell diameter should change the numbers, albeit a small amount for low flight times and small changes in diameter. Make sure you have clicked out of the diameter cell or hit enter before pressing calculate, also ensure macro's are enabled. If you want I will post a table of results for various diameters. As shell diameters start to get large 200mm+ (same mass and flight time) it starts to create some interesting results.

 

At small changes in shell diameter 3" to 8" at the same mass and flight time you will see an interesting trend in the muzzle velocities due to the non linear nature of drag. But you will see lower apogees and lower times to apogee as expected.

 

Try some higher flight times and you will start to see the effect of drag more. For instance here are the results from a 3" 150 gram shell and an 8" 1kg shell at 20 seconds flight time.

 

3", time to apogee 6.8s, height of apogee 373m, muzzle velocity 135.7m/s, impact velocity 34.9m/s

8", time to apogee 8.2s, height of apogee 493.5m, muzzle velocity 215m/s, impact velocity 68.23m/s

 

OK that is an extreme example. however we have tested flight times for dummy 3" shells (cricket balls) and with small amounts of lift (less than 10g IIRC, but someone who participated may remember better than me) it is possible to get flight times in excess of 20 seconds.

 

If it is still not working for you we will try and sort it out.

 

Cheers

 

Gareth

[dave]

hmm, changed the velocity , mass , flight time and size, and clicked calculate
 
came up with
 
"=EMBED("Forms.CommandButton.1","")

[digger]

What version of excel are you using?

[digger]

I wrote this a long time ago. I will update it for XLSM files and repost.

[digger]

I have tried it in Excel 2003 and 2007.

 

It sounds like you have an Active X issue or macro's are disabled.

 

Find attached a copy in the newer XLSM format the first uses active X controls and the second uses form controls.

 

You will need to change the file extension from XLS to XLSM in both cases as the form won't allow me to upload XLSM files.

 

Let me know which one works for (if any) for you.

Attached Files

•  shell height active x.xls   26.17KB   416 downloads
•  shell height form control.xls   24.1KB   339 downloads

Edited by digger, 26 October 2014 - 06:36 PM.